孙鑫与合作者在二维渗流模型的研究中取得重要进展
近日,北京大学北京国际数学研究中心孙鑫和香港城市大学Pierre Nolin、钱玮,以及宾夕法尼亚大学庄子杰几位研究人员,在二维渗流模型的研究中合力取得重要进展。四人撰写的论文Backbone exponent for two-dimensional percolation于2023年9月发布于arXiv预印本网站,随后在相关领域引起强烈反响。物理学家Ilya Gruzberg和Greg Huber在凝聚态物理期刊俱乐部为该文撰写了评论[1],著名科普杂志Quanta Magazine对该成果的背景和产生过程做了详尽报道[2]。
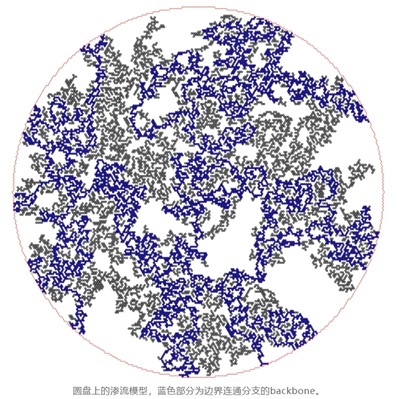
渗流模型是一个经典的统计物理格点模型,该模型的臂指数是刻画其临界状态的重要指标,根据颜色样式可分单色、多色两类。利用共形场论等工具,物理学家对二维情形的多色臂指数和一臂指数有精确预测。根据Smirnov的开创性工作,二维临界渗流模型的连续极限可被SLE曲线描述。由此数学家Lawler、Schramm、Werner、Smirnov对上述物理预测给出了严格证明。
与之相对,人们对二维情形臂数至少是2的单色臂指数知之甚少,物理学无精确预测,对应的SLE问题亦很难求解。其中单色双臂指数(即backbone exponent)历史尤为悠久,与渗流连通集上的随机游动密切相关。孙鑫等人最近的文章给出了该指数的精确值并证明其是超越数,特别地,是无理数。另一方面,其他已知臂指数均为有理数。此前,人们对单色双臂指数做了数值模拟并猜测其精确值为与之相近的有理数,如17/48。因此,Gruzberg和Huber认为孙鑫等人的结果是令人惊讶的”重大突破”[1]。两人指出,虽然这一指数为无理数,但它仍然有简单优雅的刻画,其背后的机制,特别是与共形场论的可能联系仍有待挖掘。
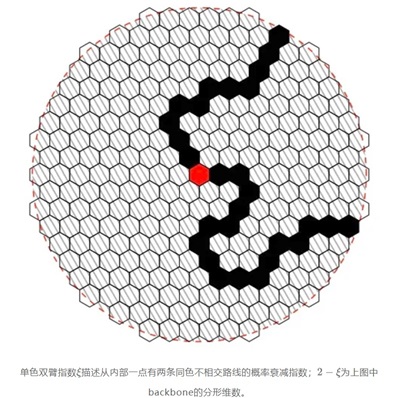
在此工作之前,孙鑫与Morris Ang、Nina Holden合作发展了利用刘维尔量子引力和SLE曲线的耦合与刘维尔共形场论可积性来得到SLE精确结果的框架。该文章首先给出了单色双臂指数的一种适用于这一框架求解的SLE描述,进而得到该指数的精确值。刘维尔量子引力是一种源于上世纪80年代弦论研究的随机曲面理论,近年来Sheffield等人构建了它的数学理论。Sheffield称四人基于刘维尔量子引力的证明是“一颗美丽的宝石”[2]。

孙鑫的主要研究方向是二维随机几何和统计物理,是相关领域的国际领军数学家,曾获概率论重要国际性奖项洛勒·戴维逊奖,2023年秋入职北京国际数学研究中心。
[1] The curious case of the backbone scaling exponent, I. Gruzberg and G. Huber, Journal Club for Condensed Matter Physics, December 31, 2023.
[2] Maze Proof Establishes a ‘Backbone’ for Statistical Mechanics, Quanta Magazine, February 07, 2024.


