Arrabit

Augmented Rayleigh-Ritz (ARR) And Block Iteration
for large-cale eigenpair computation

Introduction

Arrabit is a MATLAB solver for computing many eigenpairs of large-scale sparse (or structured) matrices. In general, the dominant computational cost in Arrabit is the matrix multiplications (A*X).

Iterations in Arrabit consist of two major steps:

a multi-power method (MPM) or a Gauss-Newton (GN) step that generates bases for approximate eigenspaces
an ARR projection step that extracts approximate eigenpairs.

Arrabit also makes use of a set of polynomial accelerators, as well as other techniques such as continuation and deflation.

Authors

Zaiwen Wen, BICMR, Peking University
Yin Zhang, CAAM, Rice University

Publication

Zaiwen Wen and Yin Zhang, Block algorithms with augmented Rayleigh-Ritz projections for large-scale eigenpair computation, Arxiv:1507.06078 (pdf) (This manuscript is split into a theoretical part and a numerical part due to requests from referees)
Zaiwen Wen and Yin Zhang, Accelerating Convergence by Augmented Rayleigh-Ritz Projections For Large-Scale Eigenpair Computation, (pdf)

In the case that Arrabit is helpful in your published work, please make a reference to the above paper.

Related Publication

X. Liu, Z. Wen, Y. Zhang, An Efficient Gauss-Newton Algorithm for Symmetric Low-Rank Product Matrix Approximations, SIAM Journal on Optimization, (pdf)
Z. Wen, C. Yang, X. Liu, and Y. Zhang, Trace-Penalty Minimization for Large-scale Eigenspace Computation, Journal of Scientific Computing, (pdf)
X. Liu, Z. Wen, Y. Zhang, Limited memory block Krylov subspace optimization for computing dominant singular value decompositions, SIAM Journal on Scientific Computing (pdf) (code: “LMSVD”)

Download and install

Download

Arrabit is distributed under the terms of the GNU General Public License.

Version: beta 1 (Download)
Download test matrices

Installation

Download and unzip arrabit_beta1.zip. This should create a directory arrabit_beta1. You may move this directory to a desired location of your choice. We refer to this directory as <arrabit-root>.

Start MATLAB and add <arrabit-root/src> to your path by the command:

>> addpath <arrabit-root/src>

To verify the Arrabit installation, go to <arrabit-root/examples> and execute the following command:

>> demo_eig

A Typical Demo Result from “demo_eig”

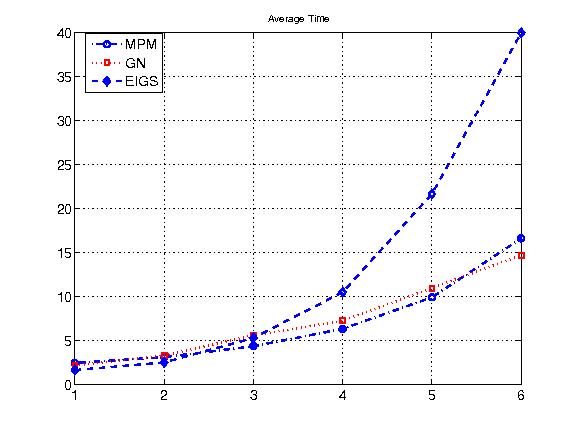(The figure is a comparison of the runtime versus the growth of the matrix dimension between two variants of Arrabit 'MPM’ and 'GN’ and Matlab 'eigs’ in calculating a few smallest eigenvalues and their corresponding eigenvectors.)

Known Issues

The performance of Arrabit may be determined by the efficiency of the matrix-matrix multiplications AX.

Sparse matrix-dense vector products using intel MKL

In Matlab 2013b, dense linear algebra operations have been generally well optimized by using BLAS and LAPACK tuned to the CPU processors in use. On the other hand, we have observed that some sparse linear algebra operations in Matlab 2013b seem to have not been as highly optimized. In particular, when doing multiplications between a sparse matrix and a dense vector or matrix (denoted by ‘‘SpMM’’) the performance of Matlab's own version of SPMM can differ significantly from that of the corresponding routine in Intel's Math Kernel Library (MKL), which is named ‘‘mkl_dcscmm’’.

Download Matlab's MEX external interface for mkl_dcscmm

installation in Ubuntu 12.04 with Matlab 2013b
- configure “mexopts.sh” with link to MKL
- compile: mex -O -largeArrayDims -output sfmult mkl-sfmult-v1.cpp

usage:
- C = A*B: C = sfmult(A, B, 1)
- C = A’*B: C = sfmult(A, B, 2)

Numerical Results on A*B, where A is 5000 by 2000 and B is 2000 by 1000

seed:  88137586, A*B: err 0.00e+00, matlab-cpu: 0.23, mkl-cpu: 0.10
seed:  87017600, A*B: err 0.00e+00, matlab-cpu: 0.22, mkl-cpu: 0.11
seed:  49049047, A*B: err 0.00e+00, matlab-cpu: 0.23, mkl-cpu: 0.10