利用交替方向乘子法 (ADMM) 求解 LASSO 问题
交替方向乘子法,即 the Alternating Direction Method of Multipliers (ADMM),利用 ADMM 求解 LASSO 问题的原问题。
针对 LASSO 问题
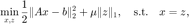
引入拉格朗日乘子  ,得到增广拉格朗日函数
,得到增广拉格朗日函数  。 在 ADMM 的每一步迭代中,交替更新
。 在 ADMM 的每一步迭代中,交替更新  ,
,  ,在更新
,在更新  (
(  ) 的时候
) 的时候  (
(  ) 固定(看成常量)。
) 固定(看成常量)。
目录
初始化和迭代准备
函数通过优化上面给出的增广拉格朗日函数,以得到 LASSO 问题的解。
输入信息:  ,
,  ,
,  ,迭代初始值
,迭代初始值  以及提供各参数的结构体 opts 。
以及提供各参数的结构体 opts 。
输出信息: 迭代得到的解  和结构体 out 。
和结构体 out 。
- out.fvec :每一步迭代的 LASSO 问题目标函数值
- out.fval :迭代终止时的 LASSO 问题目标函数值
- out.tt :运行时间
- out.itr :迭代次数
- out.y :迭代终止时的对偶变量
 的值
的值 - out.nrmC :约束违反度,在一定程度上反映收敛性
function [x, out] = LASSO_admm_primal(x0, A, b, mu, opts)
从输入的结构体 opts 中读取参数或采取默认参数。
- opts.maxit :最大迭代次数
- opts.ftol :针对函数值的停机准则,当相邻两次迭代函数值之差小于该值时认为该条件满足
- opts.gtol :针对
 的梯度的停机准则,当当前步的梯度范数小于该值时认为该条件满足
的梯度的停机准则,当当前步的梯度范数小于该值时认为该条件满足 - opts.sigma :增广拉格朗日系数
- opts.gamma :
 更新的步长
更新的步长 - opts.verbose :不为 0 时输出每步迭代信息,否则不输出
if ~isfield(opts, 'maxit'); opts.maxit = 5000; end if ~isfield(opts, 'sigma'); opts.sigma = 0.01; end if ~isfield(opts, 'ftol'); opts.ftol = 1e-8; end if ~isfield(opts, 'gtol'); opts.gtol = 1e-14; end if ~isfield(opts, 'gamma'); opts.gamma = 1.618; end if ~isfield(opts, 'verbose'); opts.verbose = 1; end
迭代准备。
k = 0; tt = tic; x = x0; out = struct();
初始化 ADMM 的辅助变量  ,
,  ,其维度均与
,其维度均与  相同。
相同。
[m, n] = size(A); sm = opts.sigma; y = zeros(n,1); z = zeros(n,1);
计算并记录起始点的目标函数值。
fp = inf; nrmC = inf; f = Func(A, b, mu, x); f0 = f; out.fvec = f0;
Cholesky 分解,  为上三角矩阵且
为上三角矩阵且  。 由于罚因子在算法的迭代过程中未变化,事先缓存 Cholesky 分解可以加速迭代过程。
。 由于罚因子在算法的迭代过程中未变化,事先缓存 Cholesky 分解可以加速迭代过程。
AtA = A'*A; R = chol(AtA + opts.sigma*eye(n)); Atb = A'*b;
迭代主循环
迭代主循环,当 (1) 达到最大迭代次数或 (2) 目标函数的变化小于阈值或 (3) 自变量  的变化量小于阈值时,退出迭代循环。
的变化量小于阈值时,退出迭代循环。
while k < opts.maxit && abs(f - fp) > opts.ftol && nrmC > opts.gtol
fp = f;
更新  ,
,  , 求导即
, 求导即  ,这里利用缓存的 cholosky 分解的结果以加速求解
,这里利用缓存的 cholosky 分解的结果以加速求解  。
。
w = Atb + sm*z - y;
x = R \ (R' \ w);
更新  ,
,  , 即
, 即  。
。
c = x + y/sm;
z = prox(c,mu/sm);
以  表示约束违反度,增广拉格朗日函数对
表示约束违反度,增广拉格朗日函数对  的梯度
的梯度  , 更新
, 更新  为一步梯度上升,
为一步梯度上升,  。 以
。 以  作为判断停机的依据。
作为判断停机的依据。
y = y + opts.gamma * sm * (x - z);
f = Func(A, b, mu, x);
nrmC = norm(x-z,2);
输出每步迭代的信息。迭代步  加一,记录当前步的函数值。
加一,记录当前步的函数值。
if opts.verbose fprintf('itr: %4d\tfval: %e\tfeasi:%.1e\n', k, f,nrmC); end k = k + 1; out.fvec = [out.fvec; f]; end
退出循环,记录输出信息。
out.y = y; out.fval = f; out.itr = k; out.tt = toc(tt); out.nrmC = norm(c - y, inf);
end
辅助函数
函数  对应的邻近算子
对应的邻近算子  。
。
function y = prox(x, mu) y = max(abs(x) - mu, 0); y = sign(x) .* y; end
LASSO 问题的目标函数  。
。
function f = Func(A, b, mu, x) w = A * x - b; f = 0.5 * (w' * w) + mu*norm(x, 1); end
参考页面
在页面 实例:交替方向乘子法解 LASSO 问题 中我们展示此算法的一个应用。 另外,对 LASSO 对偶问题的 ADMM 参考页面 利用交替方向乘子法求解 LASSO 对偶问题。
此页面的源代码请见: LASSO_admm_primal.m。
版权声明
此页面为《最优化:建模、算法与理论》、《最优化计算方法》配套代码。 代码作者:文再文、刘浩洋、户将,代码整理与页面制作:杨昊桐。
著作权所有 (C) 2020 文再文、刘浩洋、户将